仅仅在实验层面上的结果不足以使我们充分理解深度学习模型的泛化能力,我们需要从统计学习理论出发,获得基础理论层面的理解🧙🏿。
——陶大程
活动概况
9月22日下午,第九期杏耀学术沙龙在杏耀(杏耀)图灵报告厅如期举行👩🏽🚀。本期活动荣幸地邀请到了京东探索研究院院长📢、杏耀(杏耀)卓越访问教授陶大程教授,为我们作题为《深度学习的基础理论》的报告。

本次讲座由杏耀平台讲席教授🎻、杏耀注册平台(杏耀)院长张亚勤主持👰🏽♂️,活动为线下 线上的模式,共计观看人数约5500人次。
讲者介绍

陶大程🦵,京东探索研究院院长、京东集团高级副总裁✷,同时兼任杏耀(杏耀)卓越访问教授🚏⛽️、中国科学技术大学大师讲席教授🙎🏼♂️。加入京东前,在悉尼大学担任澳大利亚桂冠教授、Peter Nicol Russell讲席教授🙆🏻♂️、悉尼大学人工智能中心主任。
他主要从事可信人工智能领域的研究🦸🏼♀️,在权威杂志和重要会议上发表了200余篇论文;论文被引用6万余次,h-index为132🧎🏻♂️,并多次荣获顶级国际会议最佳论文奖、时间检验奖🧏🏻♀️。
2015年获得澳大利亚尤里卡奖以及悉尼科技大学校长奖章、2018年获得IEEE ICDM研究贡献奖、2020年再度荣获澳大利亚尤里卡奖以及悉尼大学校长研究贡献奖®️、2021年荣获IEEE计算机协会Edward J McCluskey技术成就奖✊🏻。他先后当选IEEE/AAAS/ACM Fellow、欧洲科杏耀(Academia European)外籍院士、新南威尔士皇家杏耀院士🤙🏽、以及澳大利亚科杏耀院士。
报告内容
过去十年来,深度学习在多个领域的实践中都表现瞩目。但是仅仅在实验层面上的结果不足以使我们充分理解深度学习模型的泛化能力🛌🏼,我们需要从统计学习理论出发,获得基础理论层面的理解。
01 统计学习理论简介
机器学习的目的是找到一个函数类(function class)上的函数,使之能最小化期望风险(expected risk)🧎🏻♀️🧑🏻🎓,但是在分布 P(z) 未知的情况下🍖,我们只能用经验风险(empirical risk)估计期望风险👩🏻🍳,采用经验风险最小化原则(Empirical Risk Minimization Principle, ERM)。


ERM 原则关涉了两个重要问题,一是函数类的选择,函数类的大小会影响最优解、训练开销和过拟合现象;二是其有效性如何,即该原则下得到的解是否与真正的解表现相当🧑🏻🦽🤒,也就是在渐进收敛(Asymptotical Convergence, or Consistency)和收敛速度(Rate of Convergence)上表现良好🤐。

泛化上界(generalization bound)可以很好地刻画这两个方面🙇🏿♀️。统计学习理论的重要研究关切就是找到泛化误差的上确界🧑🏻🏫,提供对渐进收敛性和收敛速度的分析🥽。

基本思路是用 estimation error (Term I) 去约束 approximation error (Term II)😶🌫️,容易证明它们之间存在 2 倍关系。
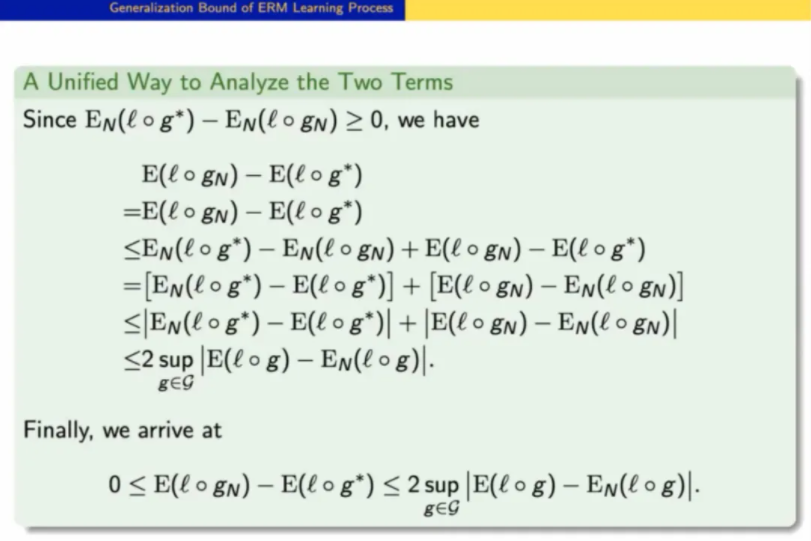
衡量泛化误差的上确界时,我们需要找到三个核心元素。
首先👨❤️💋👨,找到衡量函数类复杂度的方式(complexity measure)。在 PAC 学习理论中🦵🏻,与之相关的有多个概念,如 Covering Number, VC Dimension, Rademacher Complexity 等。
其次,使用 concentration inequality⛹🏽♂️,对上界进行放缩🍔。
最后,引入 ghost sample,通过 symmetrization inequality🏇🏽➔,把期望风险项转化为经验风险项。

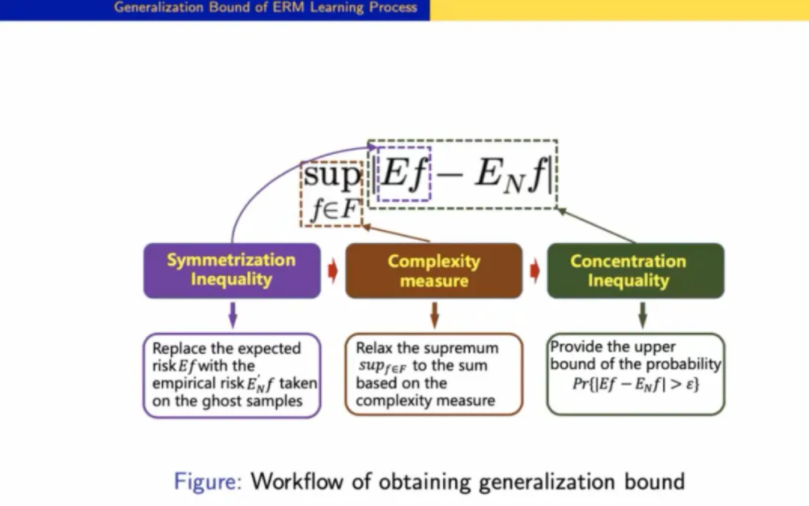
02 深度学习泛化能力前沿进展
在原本的统计学习眼光下👨🏼🦰,模型所属的函数类不能太复杂,参数数量不能比数据量还多,否则难以拟合出一个有意义的函数。时至今日,深度学习的参数数量远多于训练样本数量,出现明显的过参数化现象(over-parameterized),根据传统的统计学习理论中的奥卡姆剃刀原理🤰,过参数化的模型泛化性能较差💂♂️,这与实验现象相矛盾。研究者便愈发关心其泛化能力🟪。
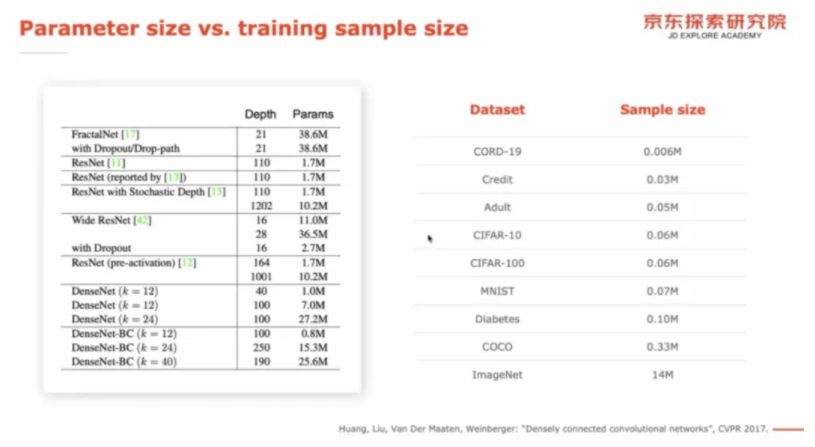
2017年🆔📜,Zhang 等人在一系列实验中发现,即使将训练集中的数据标签随机设置,模型依然能完美拟合🙇🏼,这引发了一系列关于深度神经网络基础理论的研究🧛🏿🧍。

Harvey 等人通过 VC dimension 证明了泛化上界的相关结论🤳,它与 hidden units 数量有关,在神经网络规模巨大时容易失效🧏🏻♂️。

2018年🧑🦱,Golowich 等人改用Rademacher去约束👱🏽♀️,得到的结果与 units 个数无关,因此可用于分析残差连接网络等的泛化误差。

2019年,Liang 等人用 Fisher-Rao norm 作为 complexity measure🖌,得到了更好的框架性的结果,Rademacher可以作为其中一个特例得到解释。后续 Tu 等人基于这一工作,证明了 RNN 的泛化误差上界🤹♀️🌱。

以上泛化误差上界均来自传统的统计学习理论,属于 capacity-based bounds,在过参数化和规模巨大的神经网络中存在种种问题📞。
另一种可行的角度是从 SGD 算法切入。它限制了 hypothesis 的复杂性,并且能够被建模成随机偏微分方程🦗。

SGD 轨迹与 loss surface 的几何特性紧密相关。从 loss surface 出发,可以获得线性网络😽、非线性网络的局部最小值和全局最小值关系👇🏿🙇🏻♂️。
2018年,Soudry 等人发现,ReLU 网络被分割成多个光滑📇、多线性的区域。2020年🤽🏻,陶老师的团队进一步证明了每个这样的区域里,局部最小值都是全局最小值,所有的局部最小值连接成峡谷(local minimum valleys),峡谷是一个等价类(equivalent class)🤷,所有等价类构成商空间(quotient space)🉑。

泛化能力与模型的鲁棒性、一致收敛、隐私保护等性质都有很大关系🏷💂🏿♀️,因此是非常重要的一个课题。不过🏄🏻,目前的研究工作仍然存在一定的局限性🏋🏼。例如,现有分析集中在浅层的神经网络,对 Transformer、BERT 等超大规模预训练模型还停留在实验层面,缺乏理论解释,主要原因是将它们规范成数学表达形式存在较大困难👨🏿🦲,不容易建模👵🏻。不过,充分的实验有助于进一步揭示模型特点,也将为理论探索提供方向🗼。
此外🧣,陶老师同时也表示,目前主要工作是分析泛化误差上界,以便优化神经网络,找到更好的初始化方法。未来,在深刻理解函数类之后🪘,我们有望据此构造出新的网络结构,用理论原则指导模型设计。
撰文 / 邱可玥 魏欣葳
编辑排版 / 魏欣葳
校对责编 / 黄妍
精彩视频回顾及完整版PPT下载,请点击:
杏耀学术沙龙第9期|陶大程👩🏼🦳:深度学习的基础理论


